Propagation de la chaleur

La propagation de la chaleur dans l'air

Jean-Pierre Van Dormael a eu la gentillesse de faire un article très intéressant sur le sujet. Il est profitable de prendre quelques minutes pour bien comprendre ce phénomène. En effet, il est indispensable de bien assimiler cette "mécanique" de transmission de chaleur pour concevoir correctement un moteur, choisir le fluide moteur, assurer sa propre sécurité...

On sait que le son se déplace dans l'air à environ 340 m / sec. Pour un moteur à air chaud, cette vitesse élevée permet d'admettre que, si on fait abstraction des pertes de charge dans les échangeurs, la pression instantanée est la même dans tout le moteur et à tout moment. Cette hypothèse est souvent faite dans les méthodes de calcul élémentaires des moteurs.

La vitesse de propagation de la chaleur dans l'air est beaucoup moins connue parce que les mécanismes en présence sont beaucoup plus compliqués. Essayons d'y voir un peu plus clair.

1. Les principes expérimentaux.

L'équation qui décrit la propagation de la chaleur dans une substance se déduit de trois constatations expérimentales simples et presque évidentes.

La première constatation est qu'en tout point d'une substance, la chaleur s'écoule du chaud vers le froid. La quantité de chaleur s'écoulant par seconde (c.-à-d. son courant) est proportionnelle à deux choses : la conductivité thermique de la substance et la pente avec laquelle la température décroît à l'endroit de l'écoulement.

La deuxième constatation expérimentale est que la température d'un volume contenant une substance augmente lorsqu'une quantité de chaleur y pénètre. Cette augmentation de température est bien sûr proportionnelle à la quantité de chaleur reçue et inversement proportionnelle au volume, à la densité de la substance qui s'y trouve et à sa chaleur spécifique.

La troisième constatation expérimentale est qu'aucune énergie ne se crée à partir de rien. Il en résulte un principe de continuité: la chaleur qui pénètre dans un élément de volume (selon la première constatation) doit nécessairement correspondre à celle qui en fait augmenter la température (selon la deuxième constatation). Autrement dit, en l'absence d'une source de chaleur dans le volume même, les deux chaleurs susdites doivent être égales sinon il y aurait création de chaleur spontanée, ce qui n'est pas possible.

2. Les équations.

Pour exprimer mathématiquement ces réalités physiques, nous nous contenterons d'une seule dimension de l'espace. Cela suffit à décrire ce qui se passe dans un fil ou dans un tube long et fin rempli de gaz. On indiquera par T(x,t) que la température T est une fonction de la position x dans le tube et du temps t de l'observation.

Nous ferons encore l'hypothèse simplificatrice que la conductivité thermique et la chaleur spécifique des matériaux sont des constantes. Ce n'est pas le cas mais ce n'est pas très important pour nous : ce qui nous intéresse c'est de comprendre les mécanismes physiques en présence.

On peut exprimer la première constatation ci-dessus comme suit :

δ Q = - k.S.(δ T(x,t)/δ x).δ t (1)

c.-à-d. que la quantité de chaleur δ Q (en joule) s'écoulant pendant un court laps de temps δ t (en sec) à travers une surface S (en m2), est proportionnelle à la chute de température δ T (en degrés Kelvin) constatée à l'endroit x au moment t, sur une courte distance δ x (en m) prise dans le sens de l'écoulement. Le rapport δ T(x,t)/δ x n'est autre que la dérivée partielle première de T par rapport à x, c.-à-d. sa pente. Le coefficient de proportionnalité k est la conductivité thermique de la substance (c.-à-d. sa capacité de conduire la chaleur) et le signe moins indique que l'écoulement se fait dans le sens de la chute de température.

Si on considère un petit volume de tube ou de fil, de section S et d'épaisseur Δ x, la quantité nette de chaleur qui y pénètre est égale à celle qui y entre à l'endroit x, moins celle qui en sort à (x + Δ x). On peut écrire en tenant compte des signes :

δ Q = k.S.{δ T(x+ Δ x,t)/δ x - δ T(x,t)/δ x}.δ t (1bis)

La seconde constatation expérimentale peut s'écrire de la façon suivante :

δ Q = ρ .c.δ T.S.Δ x (2)

c.-à-d. que la quantité de chaleur δ Q (en joule) qui a pénétré dans le petit volume S.Δ x (en m3), y a provoqué une augmentation de température δ T (en degrés K). Les coefficients de proportionnalité ρ (la lettre grecque rho) et c sont respectivement la densité de la substance (en kg/m3) et sa chaleur spécifique (en joule/kg/degré K). Cette dernière exprime la quantité de chaleur qu'il faut pour élever d'un degré la température d'un kg de la substance. Pour les gaz qui sont compressibles, cette quantité est différente selon que l'opération se fait à volume ou à pression constante. Nous avons utilisé ci-dessous les valeurs correspondant au volume constant.

Enfin, le troisième fait physique, celui de la continuité, s'écrit en égalant les termes δ Q des équations (1bis) et (2).

ρ .c.δ T.S.Δ x = k.S.{δ T(x+Δ x,t)/δ x - δ T(x,t)/δ x}.δ t (3)

En réarrangeant cette équation en la divisant par δ t, par (ρ .c), par S et par Δ x, on obtient :

δ T/δ t = (k/(ρ .c)).{δ T(x+Δ x,t)/δ x - δ T(x,t)/δ x}/Δ x (3bis)

Cette équation dit que la variation de température δ T (en degrés) pendant le court laps de temps δ t (en secondes) c.-à-d. la vitesse avec laquelle la température varie est proportionnelle à la variation de la pente de la température (δ T/δ x) sur la distance Δ x. Le coefficient de proportionnalité est k/ρ .c. Si on fait tendre Δ x vers zéro, l'expression{δ T(x+Δ x,t) /δ x - δ T(x,t)/δ x}/Δ x devient la dérivée partielle seconde de T par rapport à x qui s'écrit δ ²T/δ x². L'équation (3bis) devient finalement

δ T/δ t = (k/(ρ .c)).(δ ²T/δ x²) (3ter)

qui est l'équation différentielle partielle de la chaleur.

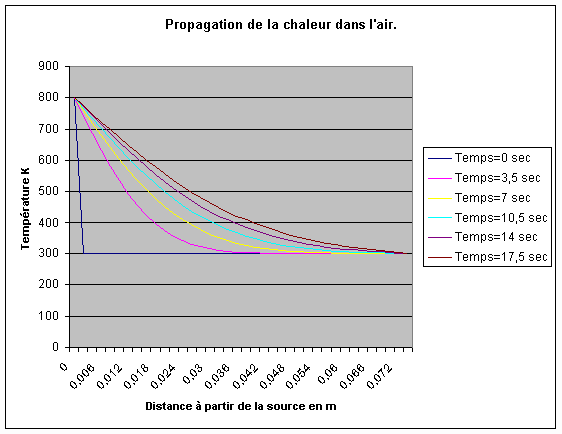
Diagramme de la propagation de la chaleur dans l'air

Cette équation permet de calculer le profil de température en fonction du temps, dans un tube isolé,rempli de gaz et terminé aux deux bouts par une source chaude et une source froide. Sa résolution n'est pas évidente. Pour ce faire, on utilise les fameuses séries harmoniques de Fourier. On n'en fera pas usage ici mais il est possible, sous certaines conditions, de résoudre numériquement l'équation avec un tableur par approximations successives au moyen de la méthode des différences finies. C'est ce que nous avons fait et voici le résultat. La source chaude à 800 degrés K est à l'extrémité gauche du tube (x = 0). Au départ tout le gaz est à 300 degrés K.

3. Et nos moteurs dans tout cela ?

L'équation (3ter) montre en tout cas que la vitesse δT/δ t avec laquelle la température varie en un point, est proportionnelle à la " constante " k/(ρ .c) du gaz utilisé. Et c'est là que l'hydrogène et l'hélium montrent une supériorité par rapport à l'air ou l'azote. Dans ce qui suit, k s'exprime en watt/mètre/degré K, ρ en kg/m2 et c en joule/kg/degré K.

Pour l'air : k/(ρ .c) = 0,025 / (1,29 x 718) = 0,000027 m2/sec).

Pour l'hélium : k/(ρ .c) = 0,14 / (0,164 x 3116) = 0,00027 m2/sec (10 fois plus que l'air).

Pour l'hydrogène : k/(ρ .c) = 0,18 / (0,083 x 10183) = 0,00021 m2/sec (8 fois plus que l'air).

Pour l'azote : k/(ρ .c) = 0,026 / (1,15 x 743) = 0,00003 m2/sec (quasi comme l'air).

A titre de comparaison avec un métal :

Pour le cuivre : k/(ρ .c) = 401/(8900 x 386) = 0,00012 m2/sec (4,4 fois plus que l'air).

Pour l'acier : k/(ρ .c) = 80,2/(7840 x 450) = 0,0000227 m2/sec (un peu moins que l'air).

Plus vite la chaleur diffuse dans le gaz, plus vite on pourra faire tourner le moteur et gagner en puissance et/ou en rendement. Lorsqu'on résout l'équation (3ter) numériquement (voir le graphique), on est surpris de constater que la vitesse de diffusion chute rapidement à moins de 3 mm / sec ! C'est plus de 100.000 fois plus lent que la vitesse du son ou de la pression. Ce n’est vraiment pas rapide. Cela montre que dans un moteur, la totalité du gaz à réchauffer ou à refroidir doit être en contact très intime avec les échangeurs. C’est ce qui fait généralement défaut dans les moteurs insuffisamment étudiés qui ont un rendement et une puissance très inférieurs à ce qu’un calcul grossier " sur un cul de lettre " laissait espérer.

Il est encore important de retenir que si on utilise de l’air ou de l’azote par exemple et que si le moteur ne tourne pas trop vite et que si les échangeurs sont efficaces sans trop de pertes de charge (= chutes de pression), de telle sorte que le gaz a le temps de s’échauffer et de se refroidir dans toute sa masse durant le cycle, il est tout à fait inutile de passer à l’hélium ou à l’hydrogène si toutes les autres conditions restent les mêmes par ailleurs. Dans ce cas, la seule façon d’augmenter la puissance d’un moteur sans changer sa configuration ou sa vitesse initiales, est d’augmenter la pression moyenne interne du gaz, quel qu’il soit. Une mise en garde s’impose ici à l’attention de ceux qui aimeraient essayer cette technique sur un modèle. L’utilisation de l’air à haute pression dans un moteur peut provoquer l’explosion des vapeurs de l’huile de lubrification par effet diesel et la destruction du moteur. Ce genre d’explosion a déjà causé la mort d’expérimentateurs chevronnés, entre autres chez Philips lors de la mise au point d'un moteur Stirling. Mieux vaut s’en tenir à des pressions faibles quand on utilise de l’air ou passer à un gaz inerte tel que l’azote ou l’hélium si on veut utiliser de fortes pressions..

Enfin, il faut encore se rappeler que la vitesse de propagation de la chaleur dans le gaz n’est pas le seul facteur pour le rendement et la vitesse de rotation d’un moteur. Il y a encore le transfert de chaleur entre les échangeurs et le gaz. La vitesse de ce transfert est grosso modo proportionnelle à la différence de température et à la surface de l’échangeur. La théorie est fort complexe mais on constate en pratique que l’échange de chaleur est inversement proportionnel à la densité du gaz. On voit que, là aussi, l’hydrogène et l’hélium ont un net avantage sur l’air ou l’azote.

Les moteurs à air chaud

La propagation de la chaleur dans l'air

1. Les principes expérimentaux.

2. Les équations.

3. Et nos moteurs dans tout cela ?